📘 DFS (Depth First Search)
📖 DFS란?
깊이 우선 탐색이라고 하며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘입니다.
📖 DFS 동작 방식
- 스택(Stack) 자료구조를 사용합니다.
- 탐색을 시작할 노드를 스택에 넣고, 방문 처리를 진행합니다.
- 방문하지 않은 근접 노드가 존재한다면 스택에 넣고, 방문 처리를 진행합니다.
- 만약 근접 노드가 모두 방문처리가 되어있다면 해당 노드를 스택에서 제거합니다.
- 위 과정을 반복해서 진행하고, 더이상 진행할 수 없을 때 탐색을 종료합니다. (스택이 비어있을 때 종료)
📖 DFS 그림으로 이해하기
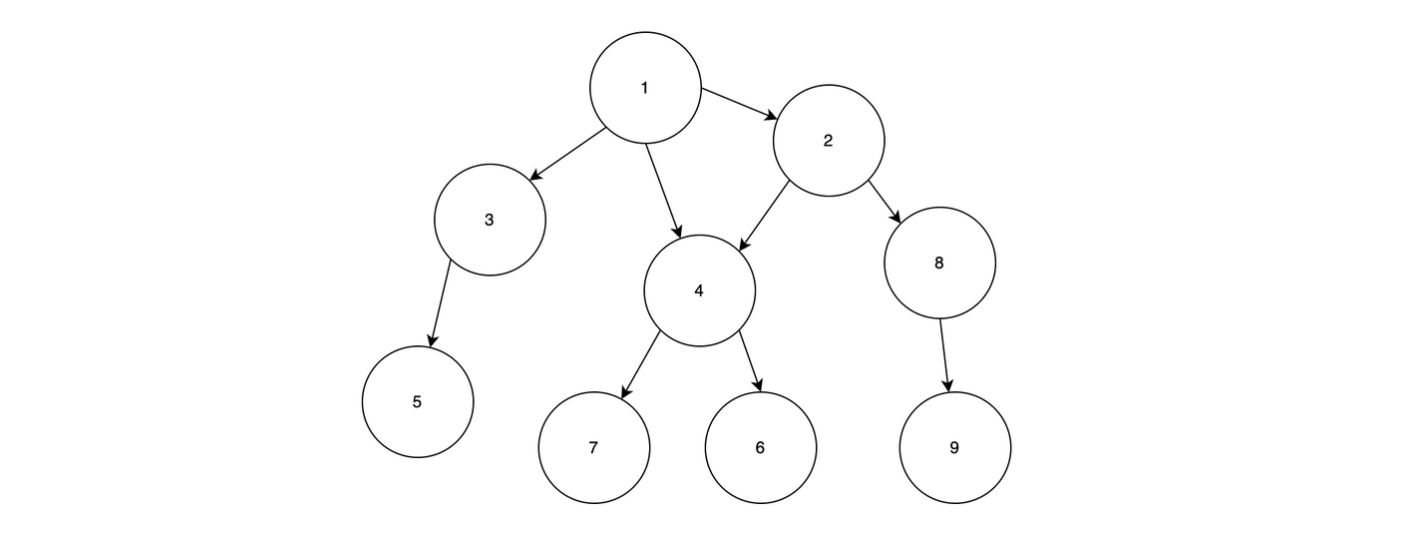
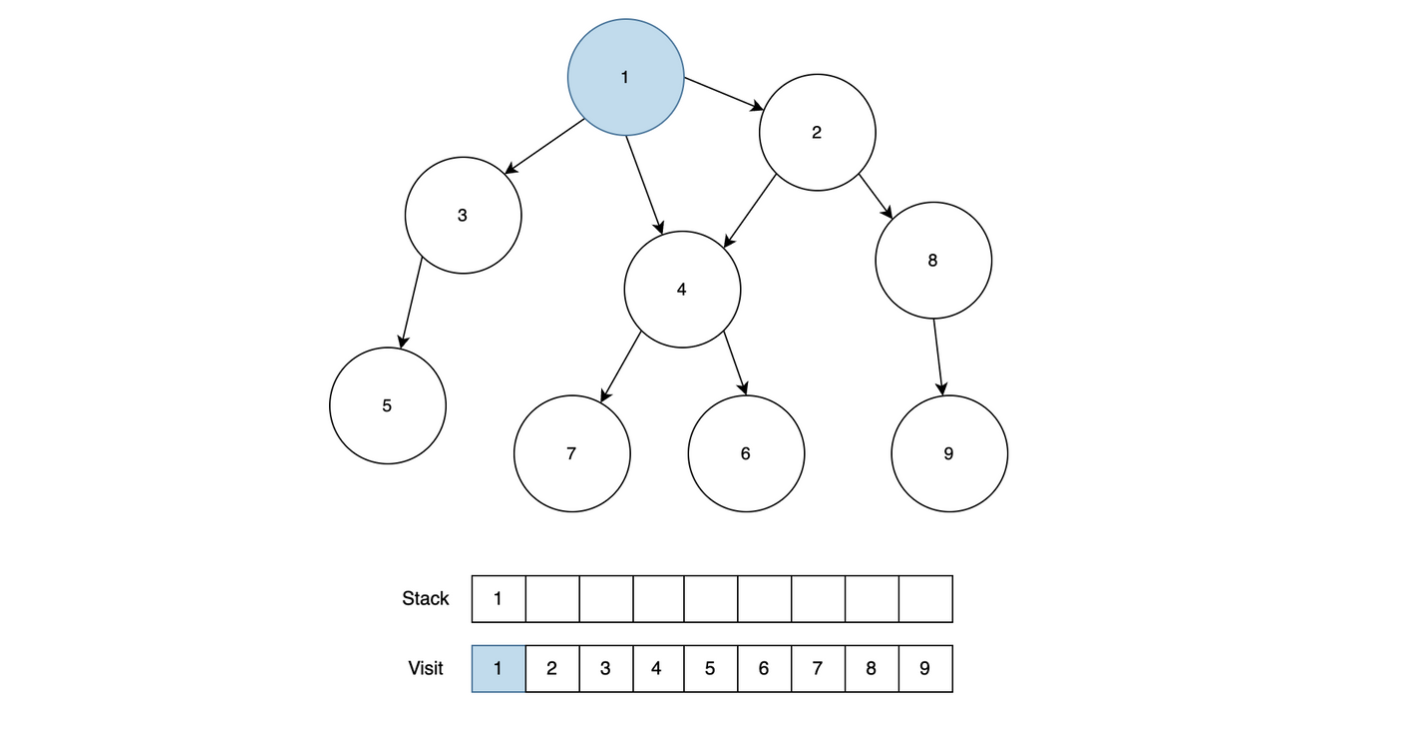
위와 같은 그래프가 존재한다고 생각해봅시다. 우리는 1번 부터 탐색을 시작할 것 입니다. 먼저 사용할 Stack과 방문처리용 Visit를 하나 만들어주고, 시작 노드 1을 스택에 넣고 방문처리를 진행합니다.
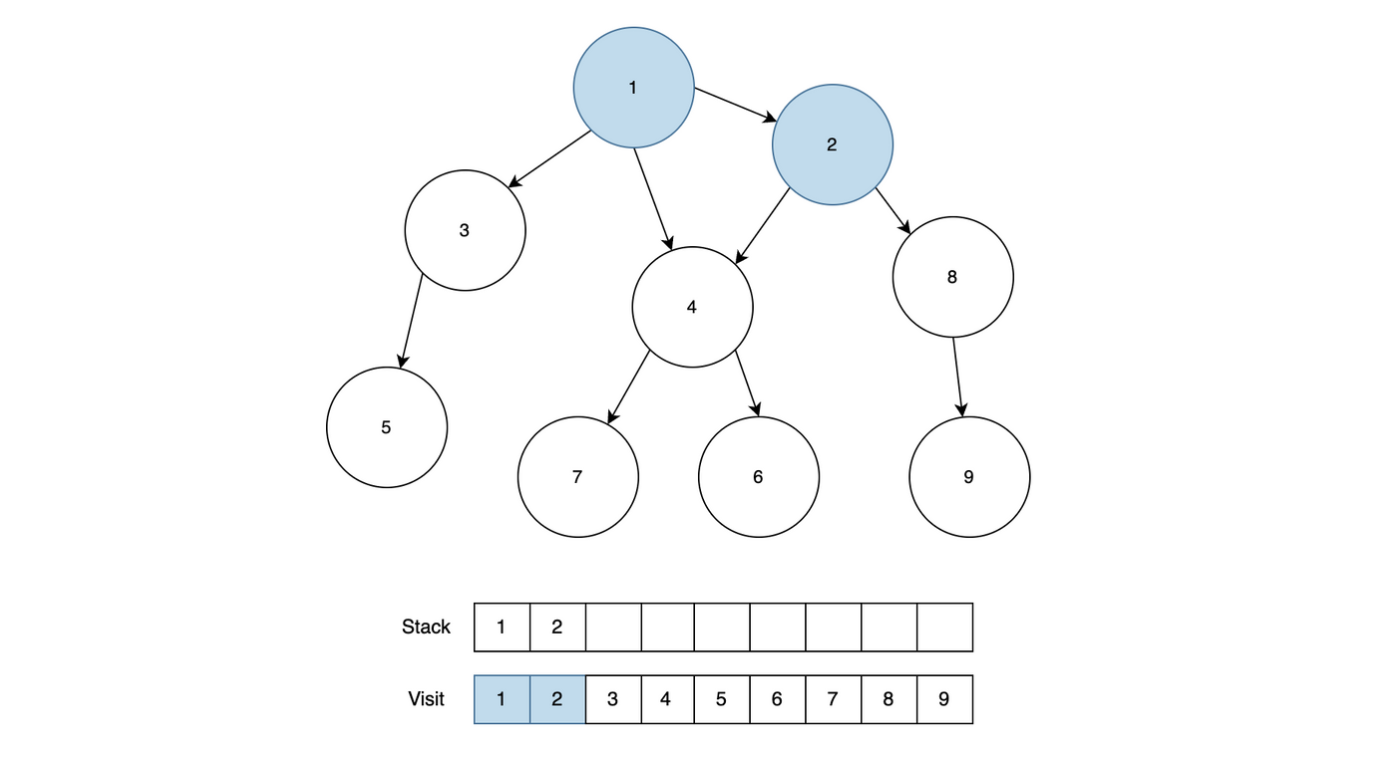
1과 근접한 노드 2, 3, 4 중에서 가장 근접한 노드 2를 다시 Stack에 넣고 방문 처리를 합니다.
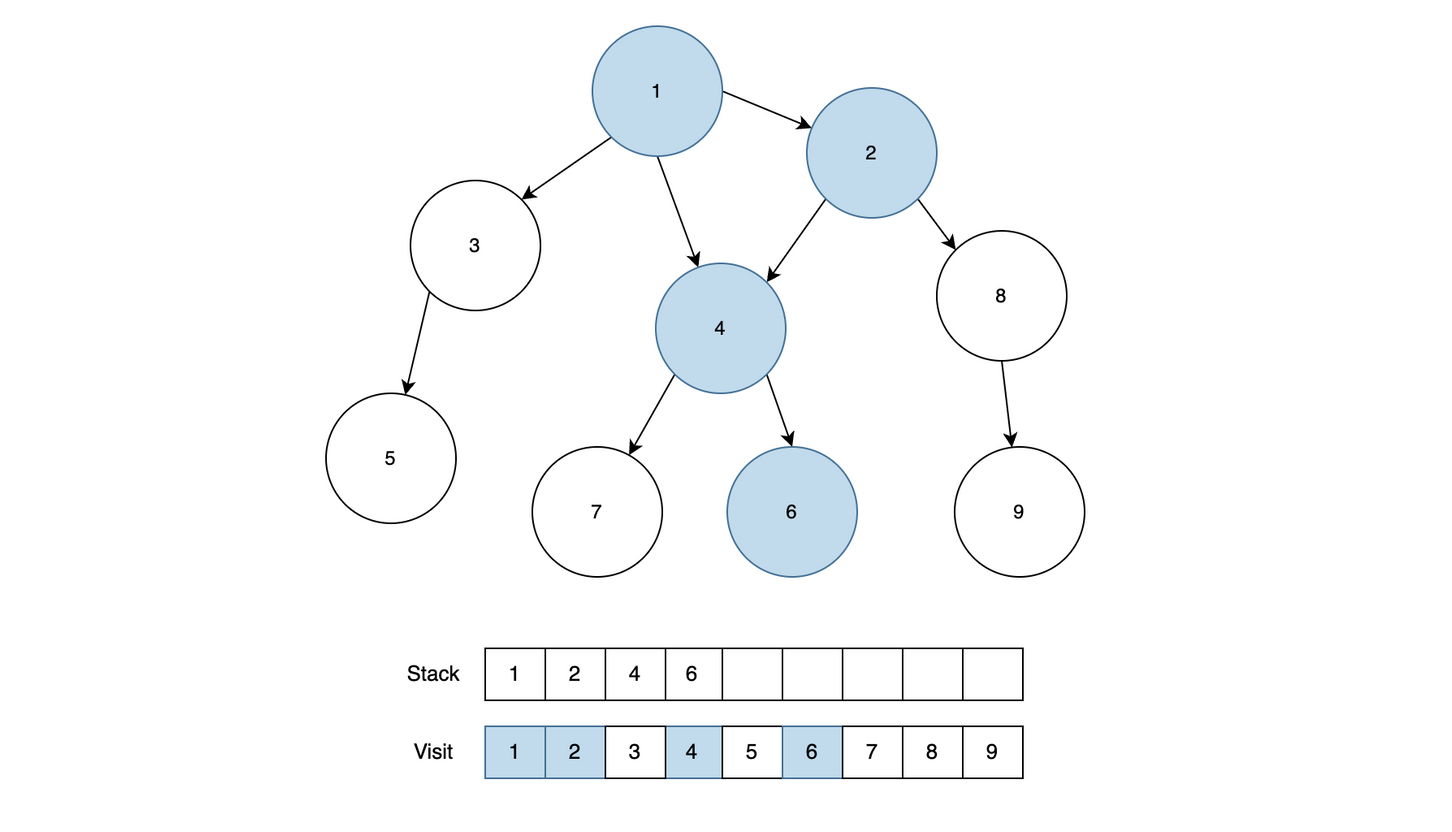
동일한 방법으로 2와 근접한 노드 1, 4, 8 중에서 근접한 노드 4(노드 1은 이미 지나온 노드이기 때문에 제외)를 스택에 넣고 방문처리를 진행하고, 바로 다음으로 4와 근접한 노드 1, 2, 6, 7 중에서 6을 스택에 넣고 방문처리를 진행합니다. 이 과정이 끝나면 아래와 같은 그래프 상태를 확인할 수 있습니다.
(이미 방문처리가 되어 있는 노드는 신경쓰지 않습니다.)
이제 가장 깊은 6까지 탐색을 끝냈기 때문에 6을 Stack에서 제거한 후 4와 근접했던 다음 노드인 7을 Stack에 넣고 방문처리를 합니다.
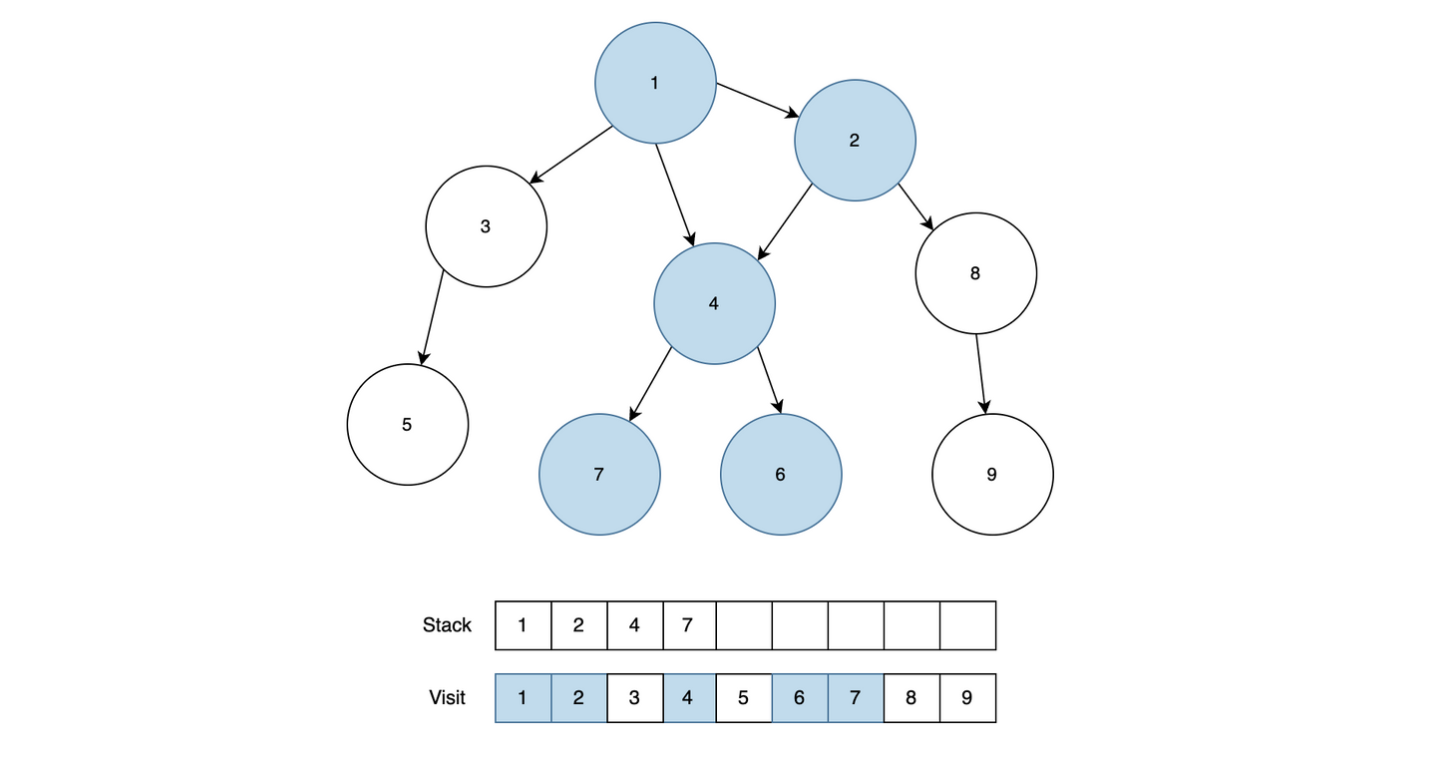
위와 같은 방법으로 7을 Stack에서 제거 한 후 4와 근접한 노드를 모두 확인합니다. 6과 7모두 방문처리가 되어있기 때문에 4도 Stack에서 제거합니다.
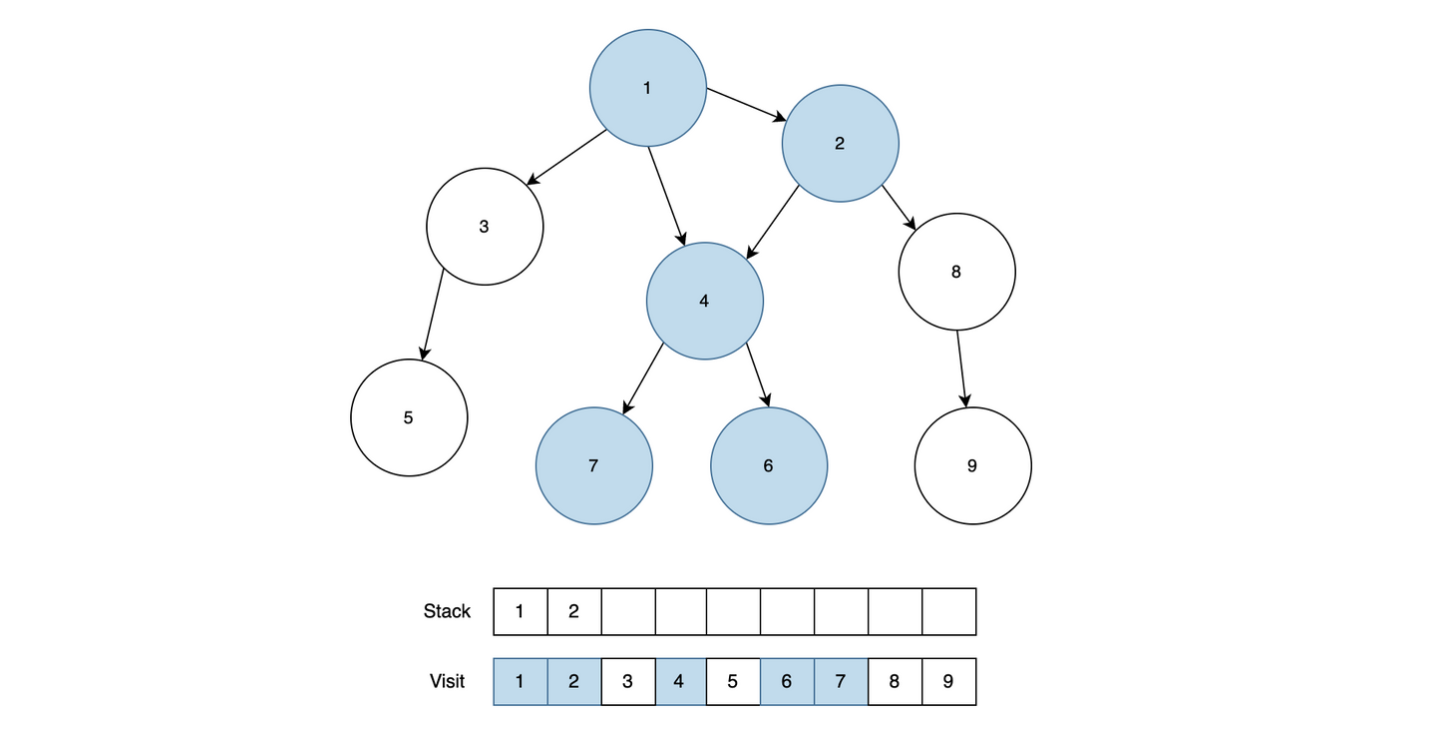
현재 노드는 2이고, 근접한 노드 4와 8 중에서 4는 이미 방문처리가 되어있기 때문에 8을 Stack에 넣고 방문처리하고, 8과 근접한 노드는 9밖에 없기 때문에 9도 이어서 Stack에 넣고 방문처리를 합니다.
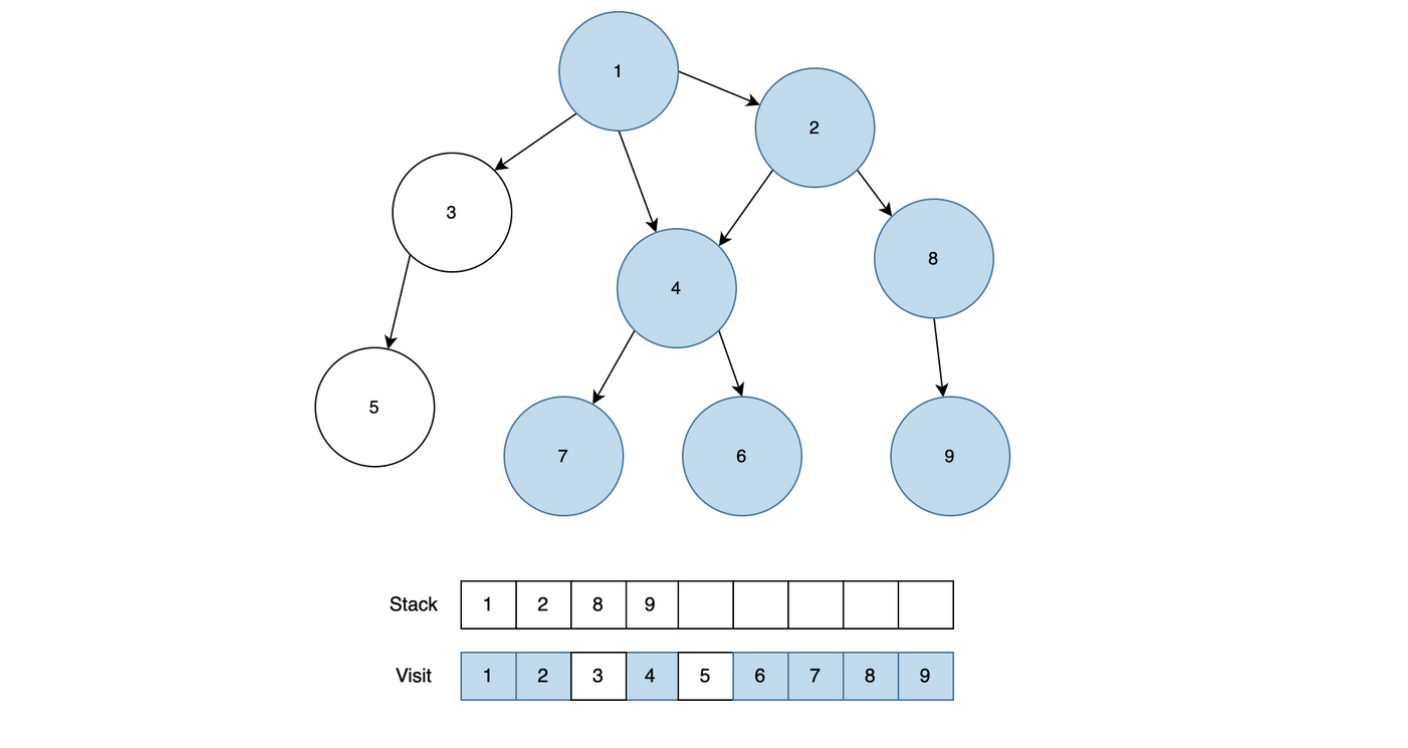
9에서는 더이상 근접한 노드가 없고, 8도 근접한 9번을 이미 탐색했고, 2도 모든 근접하는 노드를 탐색했기 때문에 1을 제외한 모든 노드를 Stack에서 제거합니다.
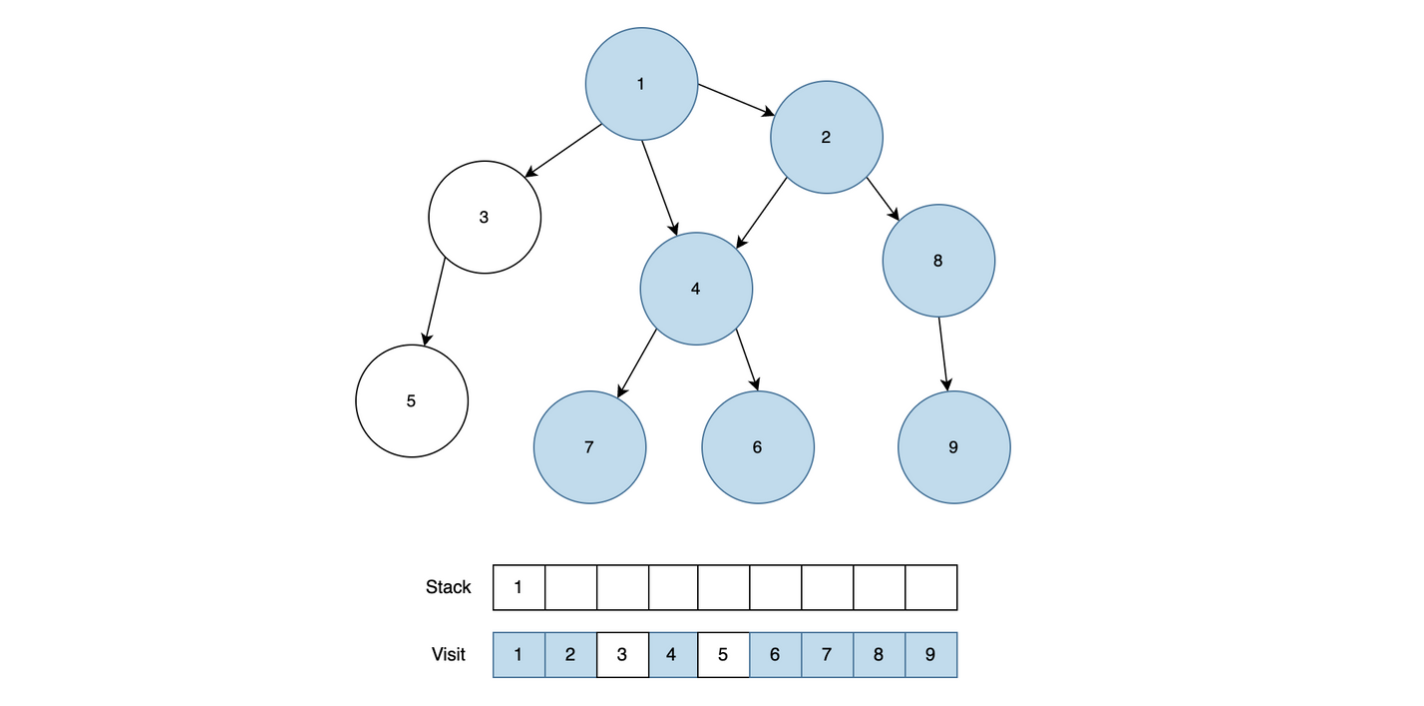
마지막으로 1과 근접한 노드 중에서 아직 방문처리가 되지 않은 3번 노드를 Stack에 넣고 방문처리를 진행하고, 3과 근접한 노드 중에서 방문처리가 되지 않은 5번 노드도 Stack에 넣고 방문처리를 진행합니다.
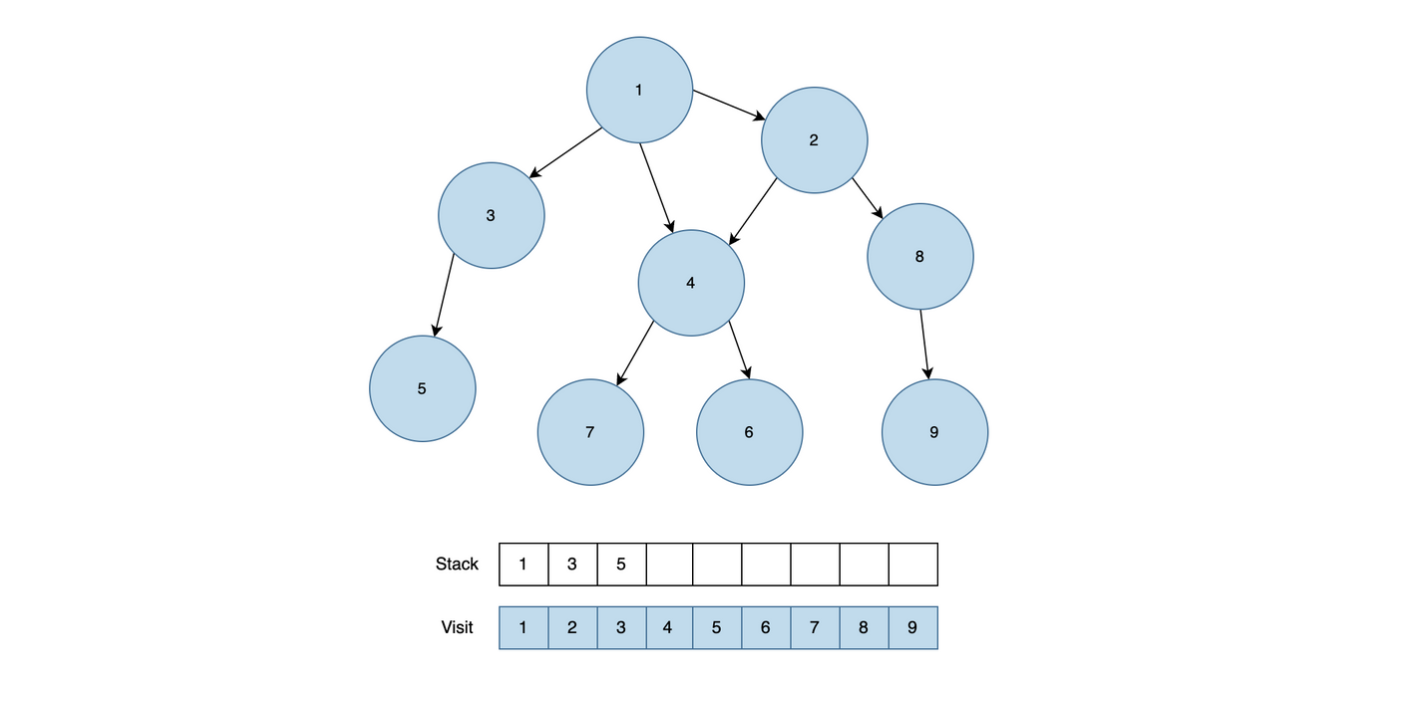
이제 모든 방문을 마친 5번 노드와 3번 노드 1번 노드 순으로 Stack에서 모두 제거되고, 탐색을 종료합니다.
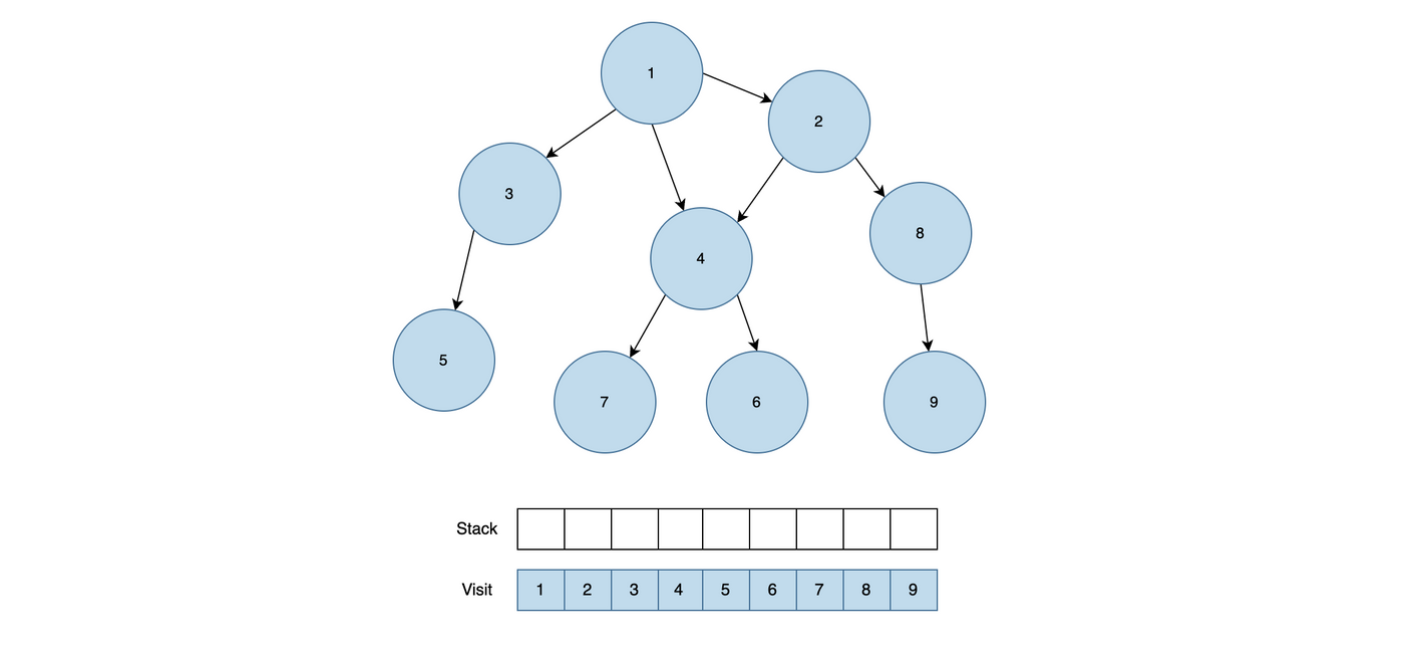
정리를 해보면 노드 탐색 순서는 1 → 2 → 4 → 6 → 7 → 8 → 9 → 3 → 5 가 됩니다.
DFS 알고리즘은 스택 자료구조를 사용하기 때문에 재귀 함수를 이용하여 구현하면 가독성도 챙기면서 코드를 구현할 수 있습니다.
📖 위 예제를 코드로 구현해보기
- 재귀함수를 이용해서 DFS를 구현해보기
public class Example {
// 0은 사용하지 않지만, 0~9까지의 노드 방문처리를 false로 초기화
public static boolean[] visit = new boolean[10];
public static int[][] graph = {
{}, // 0번 노드와 인접한 노드들
{2, 3, 4}, // 1번 노드와 인접한 노드들
{1, 4, 8}, // 2번 노드와 인접한 노드들
{1, 5}, // 3번 노드와 인접한 노드들
{1, 2, 6, 7}, // 4번 노드와 인접한 노드들
{3}, // 5번 노드와 인접한 노드들
{4}, // 6번 노드와 인접한 노드들
{4}, // 7번 노드와 인접한 노드들
{2, 9}, // 8번 노드와 인접한 노드들
{8} // 9번 노드와 인접한 노드들
};
public static void main(String[] args) {
dfs(1); // dfs 탐색 시작
}
public static void dfs(int node) {
visit[node] = true; // 해당 node를 방문처리 합니다.
System.out.print(node + " ");
for (int n : graph[node]) {
if (!visit[n]) { // 만약 근접한 노드가 방문처리가 되어있지 않은 경우
dfs(n); // 근접한 노드를 가지고 재귀함수를 실행
}
}
}
}/* 출력 결과 */
1 2 4 6 7 8 9 3 5- stack을 이용해서 DFS 구현해보기
import java.util.Stack;
public class Example {
// 0은 사용하지 않지만, 0~9까지의 노드 방문처리를 false로 초기화
public static boolean[] visit = new boolean[10];
public static int[][] graph = {
{}, // 0번 노드와 인접한 노드들
{2, 3, 4}, // 1번 노드와 인접한 노드들
{1, 4, 8}, // 2번 노드와 인접한 노드들
{1, 5}, // 3번 노드와 인접한 노드들
{1, 2, 6, 7}, // 4번 노드와 인접한 노드들
{3}, // 5번 노드와 인접한 노드들
{4}, // 6번 노드와 인접한 노드들
{4}, // 7번 노드와 인접한 노드들
{2, 9}, // 8번 노드와 인접한 노드들
{8} // 9번 노드와 인접한 노드들
};
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
dfs(1, stack); // dfs 탐색 시작
}
public static void dfs(int node, Stack<Integer> stack) {
stack.push(node);
visit[node] = true;
System.out.print(node + " ");
while (!stack.empty()) {
// 현재 노드를 가져옵니다. (아직 스택에서 제거는 하지 않음)
int currentNode = stack.peek();
// 근접하는 노드가 모두 방문처리 되어있는지 확인하기 위한 불값
boolean hasNearbyNode = false;
for (int n : graph[currentNode]) {
if (!visit[n]) { // 근접 노드가 방문처리 되어있지 않다면 방문처리를 진행
visit[n] = true;
hasNearbyNode = true; // 방문처리 되어있지 않은 노드가 존재
stack.push(n); // 스택에 해당 노드를 추가해줍니다.
System.out.print(n + " ");
break;
}
}
if (!hasNearbyNode) { // 근접 노드가 모두 방문처리되어 있다면
stack.pop(); // 해당 노드는 탐색이 모두 끝났기 때문에 stack에서 제거합니다.
}
}
}
}/* 출력 결과 */
1 2 4 6 7 8 9 3 5📘 BFS (Breadth First Search)
📖 BFS란?
너비 우선 탐색이라고 하며, 가까운 노드부터 탐색하는 방법을 말합니다. 위에서 말했던 DFS는 깊이를 우선으로 하는 탐색으로서 가장 깊은 곳까지 탐색하는 방면 BFS는 너비를 우선으로 탐색하기 때문에 넓게 탐색을 시작합니다.
📖 BFS 동작 방식
- 큐(Queue) 자료구조를 사용합니다.
- 탐색 시작 노드를 큐에 넣고, 방문처리를 진행합니다.
- 큐에서 노드를 꺼내 인접해있는 노드 중 방문처리되어 있지 않은 노드를 모두 큐에 넣고, 방문처리를 진행합니다.
- 1번과 2번을 할 수 없을 때까지 반복해서 진행합니다. (큐가 비어있으면 탐색을 종료합니다.)
📖 BFS 그림으로 이해하기
DFS에서 사용한 그래프와 동일한 그래프로 예시를 들어보겠습니다. 먼저 시작 노드 1을 큐에 넣고 방문처리를 진행합니다.
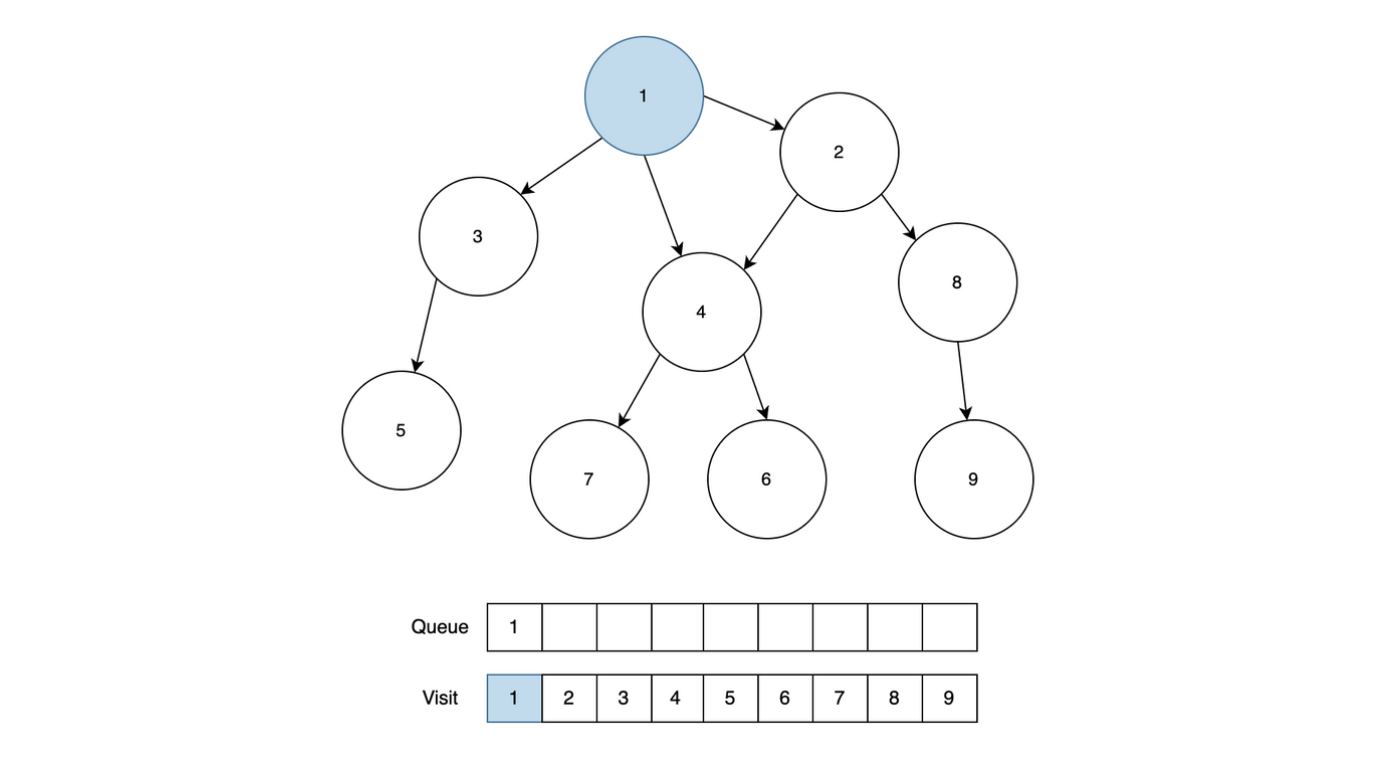
1번 노드를 Queue에서 꺼내고, 1번 노드와 근접한 노드 2, 3, 4 중에서 방문처리가 되어있지 않은 2, 3, 4 노드 모두 Queue에 추가하고, 방문처리를 진행합니다.
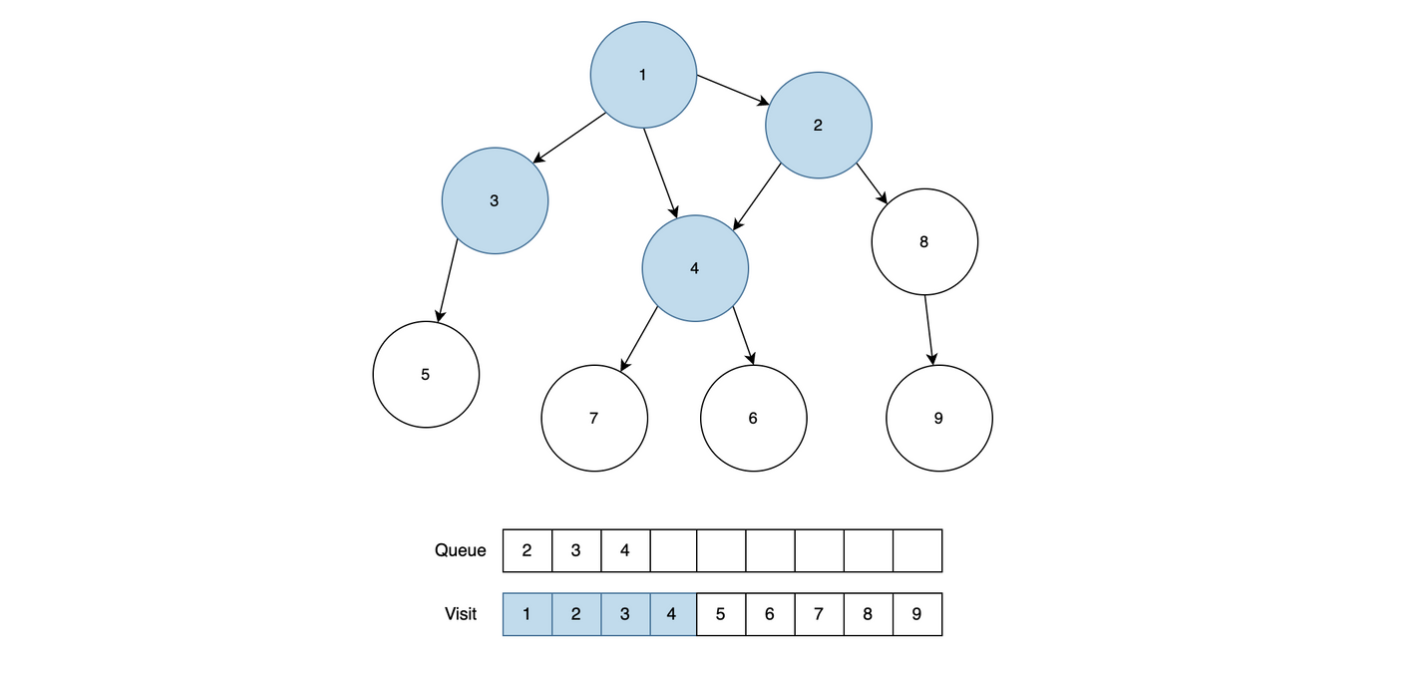
2번 노드를 Queue에서 꺼내서 근접 노드를 확인합니다. 근접 노드 1, 4, 8번 중에 방문처리가 되어있지 않은 8번 노드를 Queue에 추가합니다.
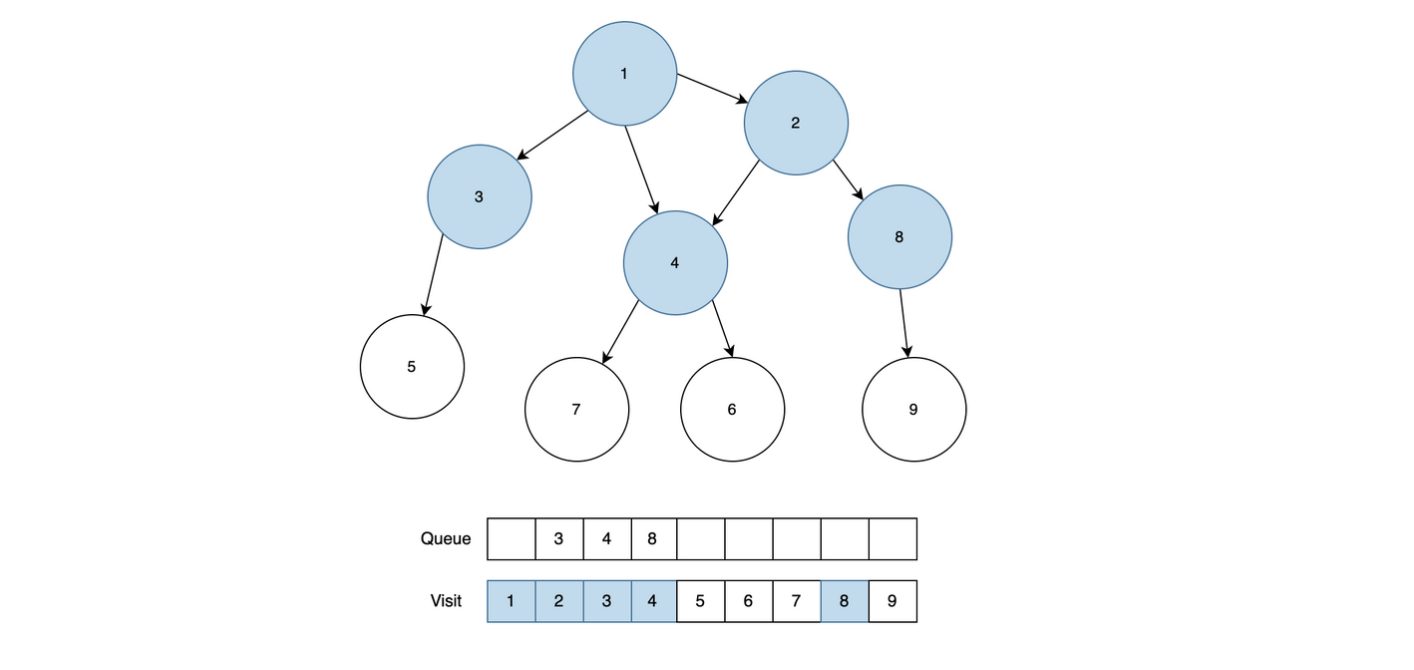
3번 노드를 Queue에서 꺼내서 근접 노드를 동일하게 확인합니다. 3과 근접노드 1, 5 중에서 방문처리가 되어있지 않은 노드 5번을 Queue에 넣고, 방문처리를 진행합니다.
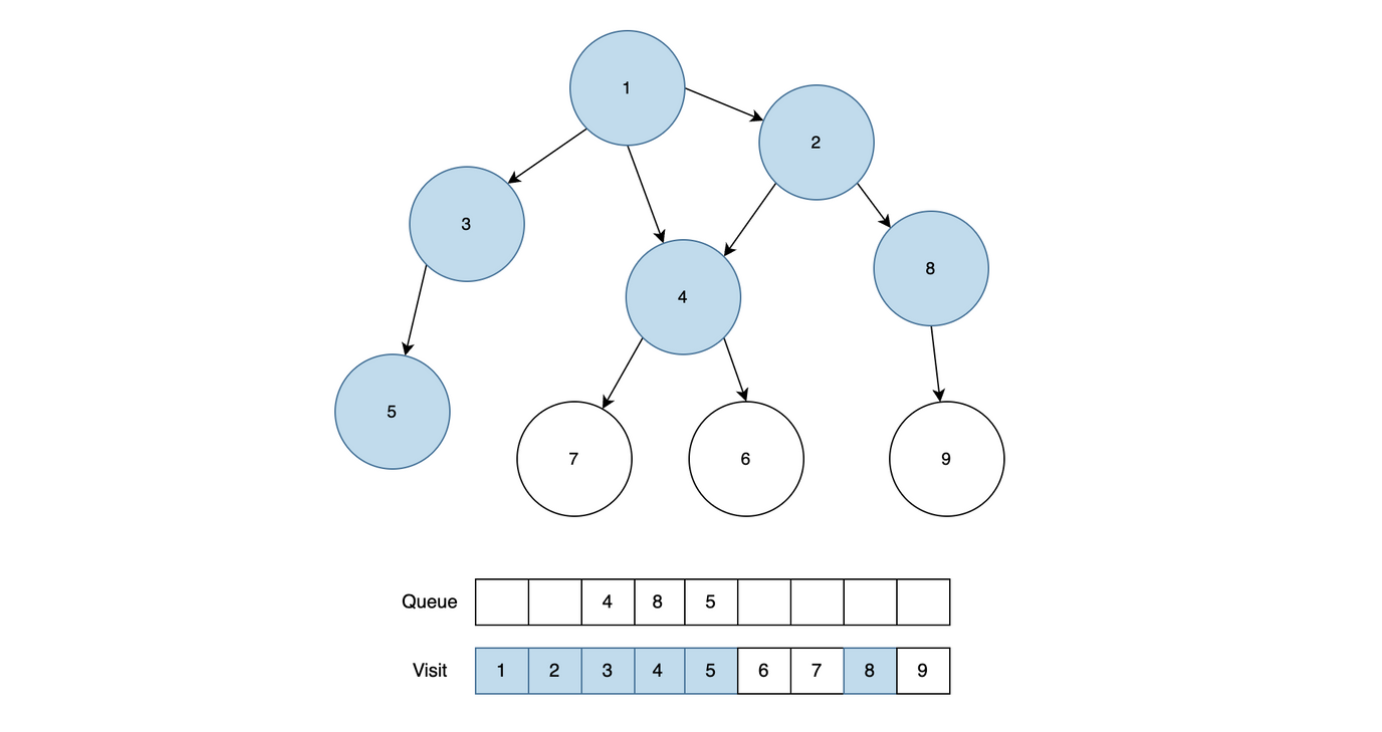
위와 같은 방법으로 계속 반복합니다. 4번 노드를 Queue에서 꺼내서 인접 노드의 방문처리 상태를 확인합니다. 6, 7번이 방문처리가 되어있지 않기 때문에 6, 7번을 Queue에 추가합니다.
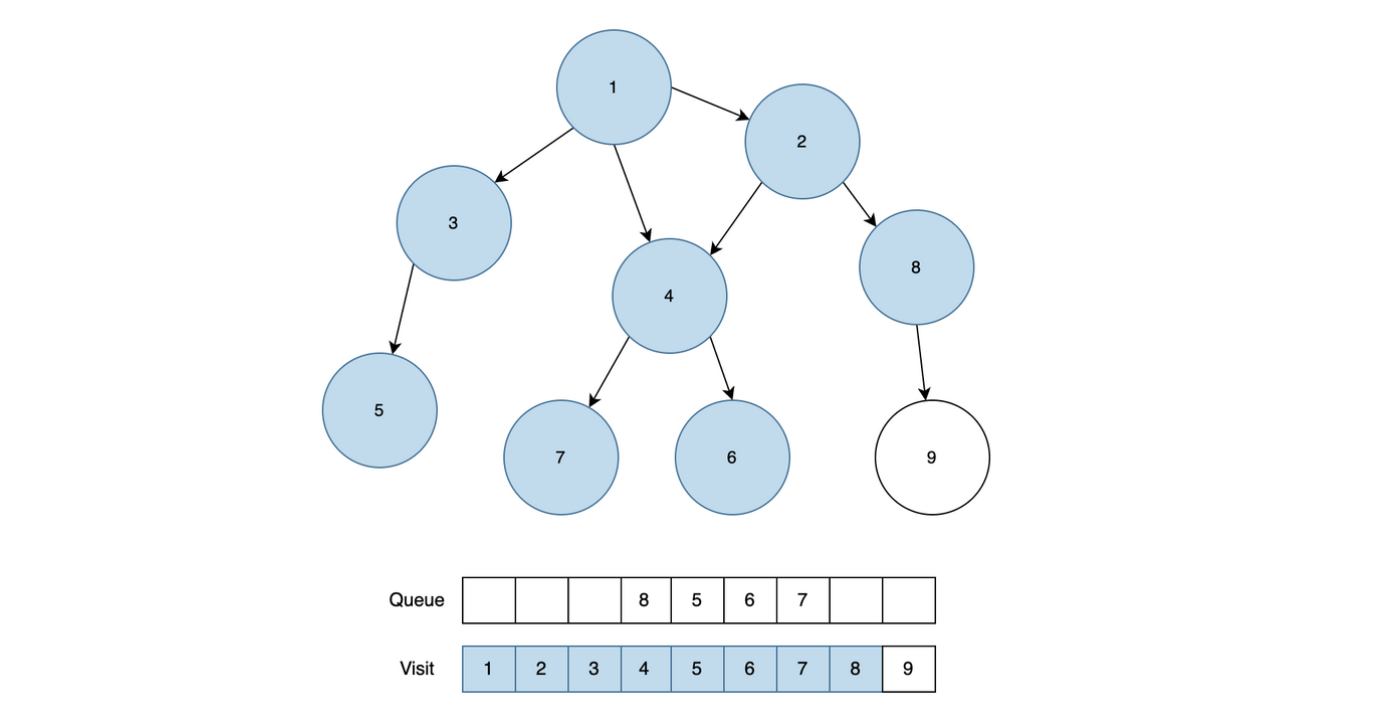
8번 노드를 Queue에서 꺼내서 인접 노드의 방문처리 상태를 확인한 후 9번 노드를 Queue에 추가합니다.
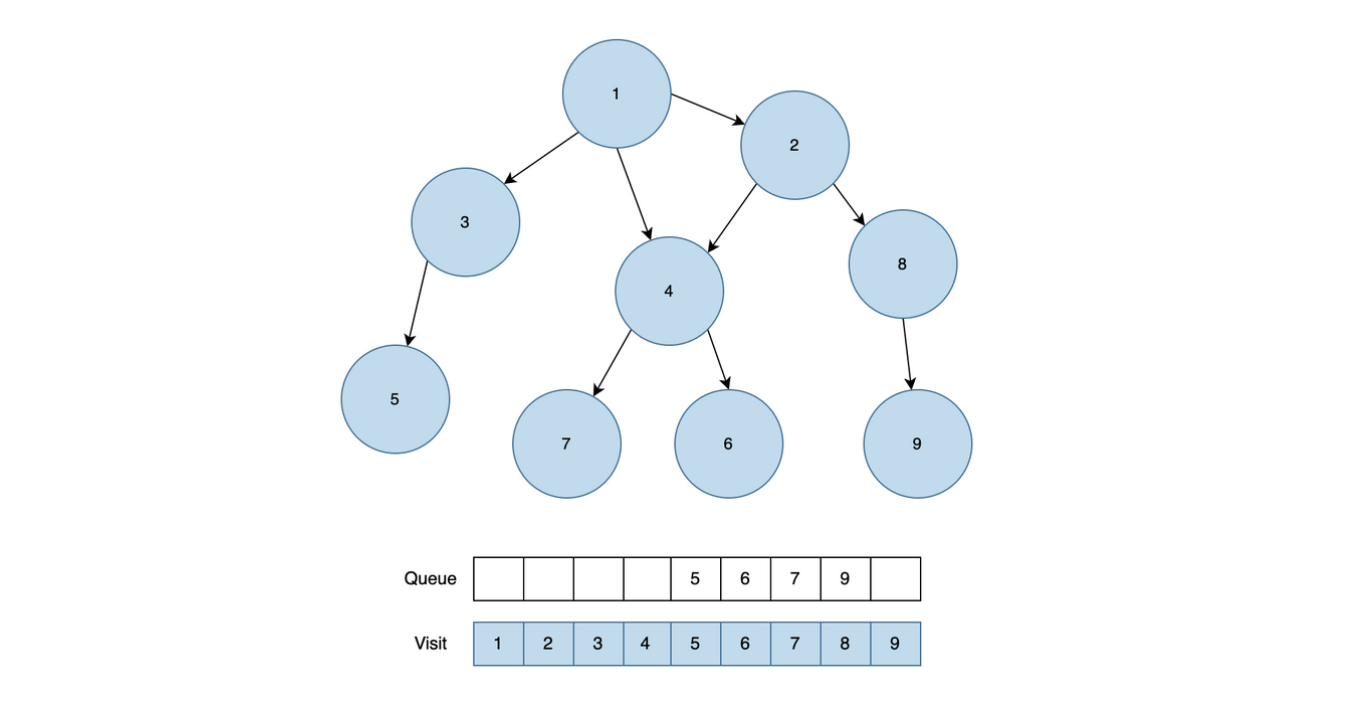
모든 방문처리가 완료되어있기 때문에 나머지 5, 6, 7, 9는 Queue에서 하나씩 제거되고, 탐색을 종료합니다.
모든 탐색이 끝나면 탐색 순서는 1 → 2 → 3 → 4 → 8 → 5 → 6 → 7 → 9 입니다.
BFS의 경우 자바에서 제공하는 라이브러리 중 Queue를 이용하여 구현할 수 있습니다. Queue는 Interface이기 때문에 구현체를 이용해서 구현해야 합니다. 일반적인 경우에는 DFS보다 BFS가 탐색 속도가 빠릅니다.
📖 위 예제를 코드로 구현해보기
- Queue를 이용하여 BFS 구현하기
import java.util.LinkedList;
import java.util.Queue;
public class BFSExample {
// 0은 사용하지 않지만, 0~9까지의 노드 방문처리를 false로 초기화
public static boolean[] visit = new boolean[10];
public static int[][] graph = {
{}, // 0번 노드와 인접한 노드들
{2, 3, 4}, // 1번 노드와 인접한 노드들
{1, 4, 8}, // 2번 노드와 인접한 노드들
{1, 5}, // 3번 노드와 인접한 노드들
{1, 2, 6, 7}, // 4번 노드와 인접한 노드들
{3}, // 5번 노드와 인접한 노드들
{4}, // 6번 노드와 인접한 노드들
{4}, // 7번 노드와 인접한 노드들
{2, 9}, // 8번 노드와 인접한 노드들
{8} // 9번 노드와 인접한 노드들
};
public static void main(String[] args) {
Queue<Integer> queue = new LinkedList<>();
bfs(1, queue);
}
public static void bfs(int node, Queue<Integer> queue) {
visit[node] = true;
queue.offer(node);
System.out.print(node + " ");
while (!queue.isEmpty()) {
int currentNode = queue.poll();
for (int n : graph[currentNode]) {
if (!visit[n]) {
visit[n] = true;
queue.offer(n);
System.out.print(n + " ");
}
}
}
}
}/* 출력 결과 */
1 2 3 4 8 5 6 7 9처음에는 DFS와 BFS 구분이 힘들었는데 DFS는 "깊이 우선 탐색"이라는 이름 처럼 탐색을 시작하면 시작한 탐색의 가장 깊은 곳까지 파고들어 탐색하고, 더이상 탐색할 곳이 없다면 다시 뒤로 돌아와서 재탐색을 시작하는 것이고, BFS는 "너비 우선 탐색"이라는 이름처럼 탐색을 시작했을 때 깊은 곳까지 파고드는 탐색이 아닌 넓게 탐색을 하는 방법이라고 이해하니 쉽게 이해했습니다.
위에서 사용된 스택과 큐가 더 궁금하다면 링크를 통해서 읽어보시면 좋을 거 같습니다!
'🧑🏻💻 Dev > Java' 카테고리의 다른 글
| [Java] 입력을 받는 BufferedReader와 Scanner (0) | 2023.02.02 |
|---|---|
| [디자인 패턴] 싱글톤 패턴 (0) | 2023.01.29 |
| [디자인 패턴] 템플릿 메서드 패턴 (0) | 2023.01.27 |
| [자바 자료구조] 스택(Stack)과 큐(Queue) (0) | 2023.01.17 |
| [자바 알고리즘] Greedy Algorithm (그리디 알고리즘) (0) | 2023.01.17 |